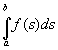dem Flächeninhalt,
das der Funktionsgraph, die x-Achse und die Parallelen zur y-Achse in a und b
einschließen. Das ist anschaulich und leicht einsehbar.
Aufgrund ihrer Bedeutung wird die Integralrechnung auch in der Schule
gelehrt. Dabei müssen die Schüler verschiedene Abstraktionsstufen
nachvollziehen und verstehen. Es sei die Funktion f(s) positiv mit a £
s £ b gegeben. In diesem Fall entspricht das bestimmte
Integral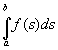 dem Flächeninhalt,
das der Funktionsgraph, die x-Achse und die Parallelen zur y-Achse in a und b
einschließen. Das ist anschaulich und leicht einsehbar.
Nun sei f(s) beliebig, insbesondere kann f(s) negativ sein. Die Schüler müssen von der greifbaren Anschauung des Flächeninhalts zum Verständnis des Integrals kommen.
Die zweite Abstraktion erfolgt mit der Einführung der
Integralfunktion. Die Integralfunktion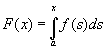 
ist Funktion des Flächeninhaltes in Abhängigkeit von der rechten
Intervallgrenze.
Dieser Prozess fordert von den Schülern ein hohes Abstraktionsvermögen und bereitet den meisten große Schwierigkeiten. Funktionen werden etwas konkreter,
sobald sie graphisch dargestellt werden. Darum bietet es sich an, die Zusammenhänge im Unterricht Computer-unterstützt zu visualisieren und so den abstrakten
Integralbegriff greifbarer zu machen. Dieses Ziel setzt sich die vorliegende Facharbeit.