2.3.3  Die Integrationsformel von Newton-Côte

2.3.3.1 Herleitung

Die Interpolation der Funktion f können wir jetzt mit Hilfe von Lagrange durchführen. P sei das interpolierende Polynom vom Grad £ n auf dem Intervall [a; b] bei n+1 äquidistanten Stützstellen x_i. Deswegen gilt:

P(x_i) = f_i := f(x_i) für i = 0, 1, . . ., n.

Die Schrittweite h ist die Länge eines Teilintervalls und beträgt:  . 

Für die Stützstellen x_i gilt daher:

Integrieren wir das interpolierende Polynom P, 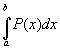=  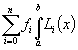=  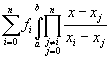, dann zeigt sich, dass die Hilfspolyome L_i nach Lagrange von den Intervallgrenzen a und b abhängen. Deswegen müssen sie bei der Integration mehrerer Integrale auf unterschiedlichen Intervallen jedesmal neu berechnet werden. Wären alle Funktionen auf [0; n] zu integrieren, könnte man stets dieselben Hilfspolynome L_i verwenden, da diese nur vom Intervall [0; n] abhängen. Diese Tatsache wollen wir ausnutzen.

Es gibt eine Transformation g(s), die das Intervall [0; n] auf [a; b] abbildet.

mit (0 £ s £ n)

Wir suchen nun eine Funktion auf [0; n], die nach [a; b] transformiert gerade f(x) ergibt.

Diese finden wir durch die Substitution . Man kann nachprüfen, dass f(g(s)) wegen der Transformationseigenschaft von g(s) die geforderte Eigenschaft erfüllt. Die Rücktransformation erhält man durch die Umkehrung von g(s):

        ®                       ®               .

Wir können nun 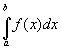  mit Hilfe der Substitution integrieren und mit g^-1(a) = 0, g^-1(b) = n und ergibt sich

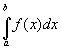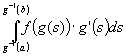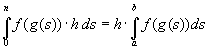== (5)

Man kann sich die Substitution auch folgendermaßen klarmachen:

Das Integral im Intervall [a; b] wird durch auf das Intervall [0; n] abgebildet, was einer Translation um -a und eine Streckung um = bedeutet.

Es ist klar, dass die Translation um -a den Wert des ursprünglichen Integrals nicht verändert. Es wird allerdings um gestreckt, d. h., um das Integral auf [a; b] zu bekommen und die Streckung aufzuheben, müssen wir 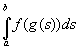mit multiplizieren (siehe (5)).

Jetzt wenden wir diesen Trick auf die Hilfspolynome nach Lagrange (3) an. Es gilt:

x – x_j = a + hs – a – hj = h(s – j)

x_i – x_j = a + hi – a – hj = h(i – j)

Deswegen erhält man für die Lagrangepolynome L_i

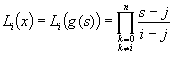. (6)

Integrieren des Interpolationspolynoms P(x) (4) unter Ausnutzung von (5) liefert dann

=

=

  =

=

=

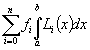
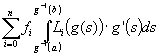
= (7) mit

(8)

Die Koeffizienten werden "Gewichte" genannt. Sie hängen, wie wir es beabsichtigt haben, nicht mehr von den Intervallgrenzen a und b ab und auch nicht von der zu integrierenden Funktion, sondern nur von n.

Es sind rationale Zahlen mit folgender Eigenschaft:

(9)

Dies lässt sich leicht nachweisen. Für die konstante Funktion f(x) = 1 ist das interpolierende Polynom P(x) = 1. Das bestimmte Integral im Intervall [0; n] ergibt

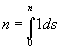= == . q.e.d.

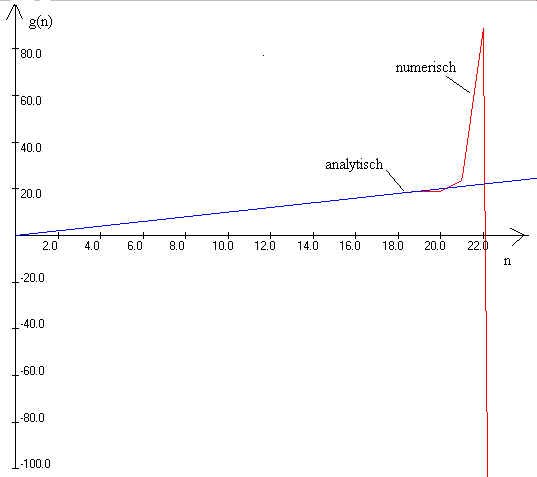
Für alle natürlichen Zahlen n bekommt man eine Integrationsformel. Allerdings werden die Gewichte für "höhere" Werte von n numerisch unbrauchbar. Das konnte auch mit dem angefertigten Computerprogramm nachgeprüft werden. Auf der Abbildung der folgenden Seite sind die Graphen zu sehen. Bis zu einem Wert von ca. 19 stimmt die numerische Berechnung mit der Formel ungefähr überein. Danach liefert die Formel aufgrund der begrenzten Rechengenauigkeit von Computern numerisch unbrauchbare Gewichte.