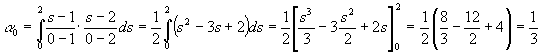
2.3.3.3 Die Newton-Côtes Formel für quadratische Approximationen – Die Regel von Simpson
Benutzen wir nun die Integrationsformel für n = 2, was einer quadratischen Interpolation gleichkommt. Zunächst berechnen wir wieder die Gewichte nach (8):
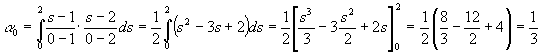
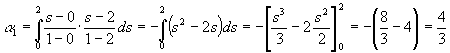
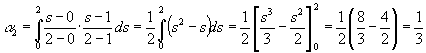
Wenden wir (7) an, so ergibt sich
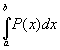 =
= ![]() =
=
= ![]()
Legen wir dem Verfahren eine wie unter 2.1 definierte Zerlegung von [a; b] in k Teilintervalle zugrunde, dann können wir schreiben:
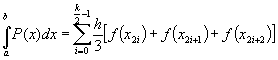
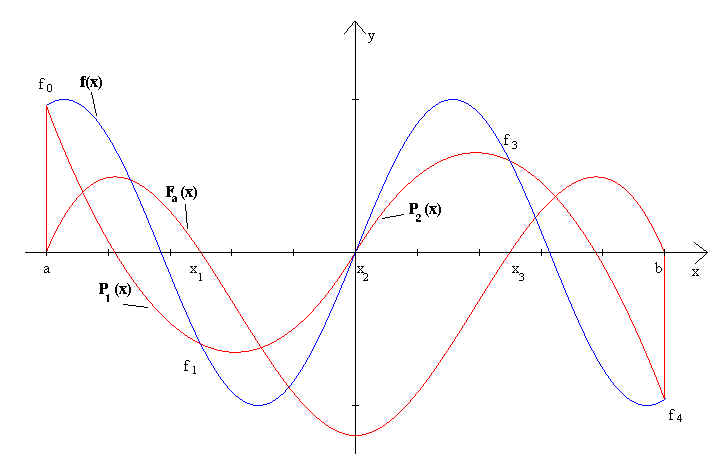
Damit haben wir genau die Simpson Regel hergeleitet. In Abbildung auf der nächsten Seite ist mit dieser Integrationsformel die Funktion f(x)=sinx durch zwei Näherungen P1 und P2 interpoliert. Fa(x) ist die Integralfunktion der Näherungen.