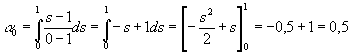
2.3.3.2 Die Newton-Côtes Regel für lineare Approximationen - Die Trapezregel
Wir wollen nun die Newton-Côtes Formel für n = 1 berechen, das bedeutet eine Interpolation durch Geradenstücke. Dazu ermitteln wir zuerst Gewichte a i nach (8):
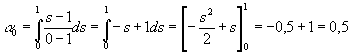
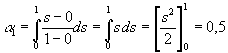
Setzen wir die Gewichte nun in (7) ein, so bekommen wir eine Näherungsformel für lineare Approximationen:
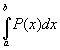 =
= ![]() =
=
= ![]()
Legen wir, wie unter 2.1 besprochen eine Zerlegung von [a; b] in mehrere Teilintervalle zugrunde, dann ergibt sich der Näherungswert
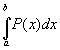 =
= ![]()
und somit die Trapezregel.
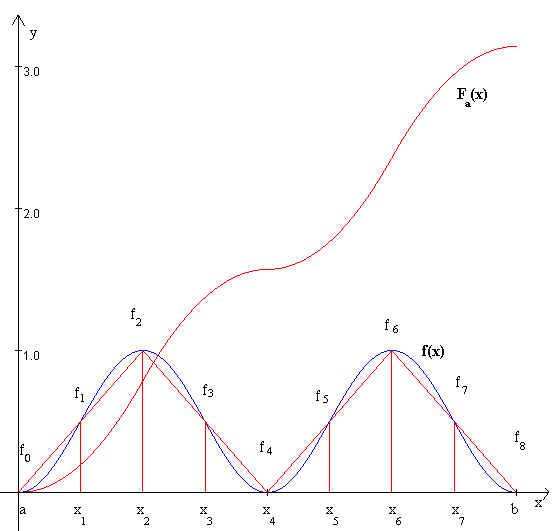
Die untere Abbildung zeigt die Funktion f(x)=(sinx)2. Es wurde eine Zerlegung in acht Teilintervalle vorgenommen, auf denen f mit der Trapezregel approximiert wurde. Fa(x) stellt die gemeinsame Integralfunktion der Approximationen dar.