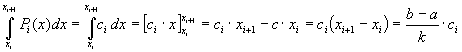2.2 Das Rechteckverfahren – Approximation durch konstante Funktionen

Ein Verfahren, das häufig zur Einführung in den Integralbegriff dient, ist das anschauliche Rechteckverfahren.

Wir betrachten die auf dem abgeschlossenen Teilintervall J = [a; b] beschränkte Funktion y = f(x). Es sei eine wie unter 2.1 definierte Zerlegung von [a; b] gegeben. Die konstante Näherungsfunktion P_i(x) = c_i gelte als Approximation für f(x) auf dem Intervall J_i = [x_i; x_i+1]. Integration von P_i(x) liefert

.

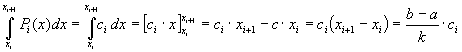Das bedeutet für das bestimmte Integral auf dem Intervall [a, b]:

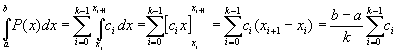
Die Parallelen zur y-Achse in x_i und x_i+1 sowie die x-Achse und ihre Parallele in c_i beschreiben ein Rechteck. Daher wird dieses Verfahren auch Rechteckverfahren gennant.

Beispiele dafür, wie man c_i bestimmen kann, sind c_i = f(x_i) oder c_i = f(x_i+1), das entspricht dem Funktionswert an der linken bzw. an der rechten Grenze von J_i. Setzt man c_i gleich dem Minimum von f auf J_i, so bekommt man die Untersumme A nach der Zerlegung Z(k).

(1)

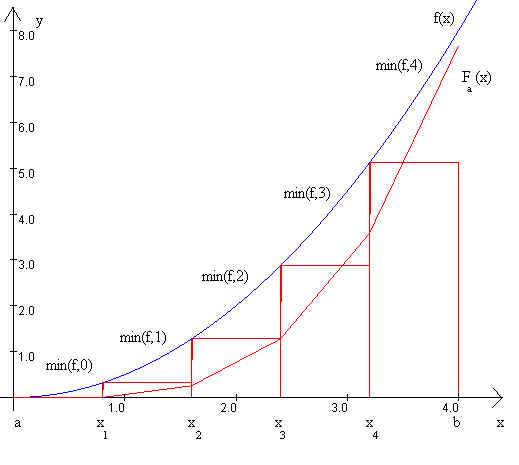
In obenstehender Abbildung wurde die Funktion nach (1) bei einer Zerlegung in fünf Teilintervalle approximiert. F_a(x) stellt die dazugehörige Integralfunktion dar.

Ebenso können wir c_i gleich dem Maximum von f auf J_i setzen, dann erhalten wir die Obersumme nach der Zerlegung Z(k):

(2)

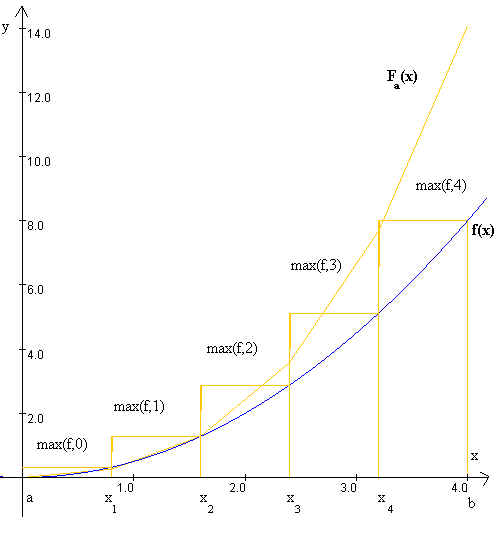
In obenstehender Abbildung wird die selbe Funktion nach (2) mit einer Zerlegung in fünf Teilintervalle approximiert. F_a(x) ist die dazugehörige Integralfunktion

Wie unter 2.1 erläutert, kann die Zerlegung verfeinert werden, um den Fehler beliebig klein werden zu lassen. Dabei fällt auf, dass die Untersumme gegen eine obere Schranke konvergiert, die das exakte Integral I repräsentiert. Das gilt ebenso für die Obersumme, die gegen eine untere Schranke konvergiert. Es gilt: