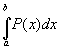 als Approximation für das bestimmte Integral
als Approximation für das bestimmte Integral 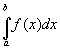 an.
an. 2.1 Prinzip
Den folgenden numerischen Integrationsmethoden liegt eine gemeinsame Idee
zugrunde: Wir ersetzen die Funktion f(x) durch eine andere Funktion P(x), die eine
Näherung für f(x) darstellt. Dann nehmen wir 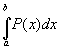 als Approximation für das bestimmte Integral
als Approximation für das bestimmte Integral 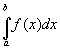 an.
an.
Da P(x) aber nur eine Näherung von f(x) darstellt, entsteht ein maximaler
Fehler von ![]() .
.
Infolgedessen ergibt sich bei der Integration ein Integrationsfehler, diesen kann man nach oben abschätzen:
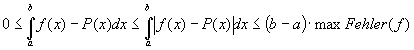
Wir können aber versuchen, den Fehler möglichst klein zu halten, indem wir im Intervall [a, b] eine Zerlegung Z(k) in k Teilintervalle vornehmen. Z(k) wird durch eine endliche Folge reeller Zahlen, den Teilpunkten der Zerlegung a = x0, x1, ... , xi, xi+1, ... xk-1, xk = b bestimmt, wobei a < x1 < ... < xi < xi+1<xk-1 < b gilt:
Z(k):=(a, x1, . . ., xi, xi+1, xk-1, b)
Die Zerlegung von [a; b] heißt dann äquidistant, wenn alle Teilintervalle gleich lang sind, also wenn x1 – a = . . . = xi+1 – xi = . . . b – xk-1. Im folgenden werden wir nur äquidistante Zerlegungen betrachten.
Ji = [xi, xi+1] sei das i-te
Teilintervall. ![]() sei die
Approximation von f auf dem Teilintervall Ji. Durch die Zerlegung Z(k) in k
Teilintervalle erreichen wir eine höhere Genauigkeit, da f auf jedem Teilintervall durch
sei die
Approximation von f auf dem Teilintervall Ji. Durch die Zerlegung Z(k) in k
Teilintervalle erreichen wir eine höhere Genauigkeit, da f auf jedem Teilintervall durch ![]() angenähert wird. Die
angenähert wird. Die ![]() sind dem Intervall Ji
"besser" angepasst, als wenn f auf [a; b] nur durch ein Interpolationspolynom
vom selben Grad angenähert würde. Der maximale Approximationsfehler ist dann:
sind dem Intervall Ji
"besser" angepasst, als wenn f auf [a; b] nur durch ein Interpolationspolynom
vom selben Grad angenähert würde. Der maximale Approximationsfehler ist dann:
![]()
Machen wir die Zerlegung immer feiner, so geht der Fehler gegen Null.
![]()
Für den Integrationsfehler können wir daraus folgern, dass er, abhängig von k ebenso beliebig klein wird.
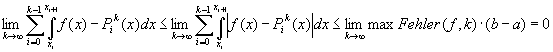
Wir können also durch die Zerlegung Z(k) des Intervalls in k kleinere
Teilintervalle 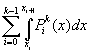 beliebig
genau an
beliebig
genau an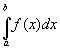 annähern.
annähern.